Continued fractions off�er a useful method and representation of expressing numbers and functions. One of interesting ideas of this method is that any number can be represented by a point on the real line and that falls between two integers.
Several attempts have been made during the last 100 years to develop continued fraction algorithm for complex numbers[1]; such algorithm having properties that are known to possess on the regular continued fraction algorithm in the real numbers case.
In the real case, for example, let  be any real number, and if
be any real number, and if 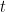 is an integer, then
is an integer, then
 .
.
There is one and only one such integer 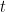 for any given real
for any given real  . The integer
. The integer 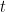 is sometimes called the floor of
is sometimes called the floor of  ,
,
![t= \left [ s \right ]](https://s0.wp.com/latex.php?latex=t%3D+%5Cleft+%5B+s+%5Cright+%5D&bg=ffffff&fg=000000&s=0&c=20201002)
For example : ![3= \left [ \pi \right ]](https://s0.wp.com/latex.php?latex=3%3D+%5Cleft+%5B+%5Cpi+%5Cright+%5D&bg=ffffff&fg=000000&s=0&c=20201002) ,
, ![-2= \left [-1.5 \right ]](https://s0.wp.com/latex.php?latex=-2%3D+%5Cleft+%5B-1.5+%5Cright+%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
For any real  with
with ![t= \left [ s \right ]](https://s0.wp.com/latex.php?latex=t%3D+%5Cleft+%5B+s+%5Cright+%5D&bg=ffffff&fg=000000&s=0&c=20201002) , there is a unique decomposition
, there is a unique decomposition  where
where 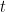 is an integer and
is an integer and  is in the unit interval. So,
is in the unit interval. So,  if and only if
if and only if  is an integer.
is an integer.
The process of finding the continued fraction expansion of a real number is a recursive process that procedes one step at a time. Given any real number  , after
, after  steps, the process goes like this one :
steps, the process goes like this one :
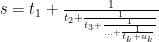
Which has integers  and real numbers
and real numbers 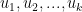 that are members of the unit interval
that are members of the unit interval 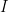 with
with 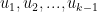 all positive. We can write another representation :
all positive. We can write another representation :
![s= \left [t_1,t_2,t_3,...,t_k+u_k \right]](https://s0.wp.com/latex.php?latex=s%3D+%5Cleft+%5Bt_1%2Ct_2%2Ct_3%2C...%2Ct_k%2Bu_k+%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
If  , the process ends after
, the process ends after  steps. Otherwise, the process continues at least one more step with
steps. Otherwise, the process continues at least one more step with
 .
.
In this way one associates with any real number  a sequence, which could be either finite or infinite,
a sequence, which could be either finite or infinite,  of integers. This sequence is called the continued fraction expansion of real number
of integers. This sequence is called the continued fraction expansion of real number  . For example,
. For example,  can be represented as a continued fraction
can be represented as a continued fraction

or ![\pi = \left [3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3 ...\right]](https://s0.wp.com/latex.php?latex=%5Cpi+%3D+%5Cleft+%5B3%2C+7%2C+15%2C+1%2C+292%2C+1%2C+1%2C+1%2C+2%2C+1%2C+3+...%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Continued fractions have become more common in various other areas since the beginning of the twentieth century. For example, Robert M. Corless [2] examines the connection between theory of chaotic dynamical systems and continued fractions. It has also been used in computer algorithms for computing rational approximations to real numbers, as well as for solving Diophantine approximation of complex numbers [1] .
It turns out that complex numbers can also be represented as continued fractions, and, as such, falls between two Gaussian integers, and the unit is any divisor of  whose norm is 1.
whose norm is 1.
The best method at the moment was devised by Asmus Schmidt. [1]
Let
![\mathbf{Z}\left [ i \right ] = \left\{a + bi : a, b \in \mathbf{Z},b \geq 0 \right\} \cup \left\{ \infty\right\}](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BZ%7D%5Cleft+%5B+i+%5Cright+%5D+%3D+%5Cleft%5C%7Ba+%2B+bi+%3A+a%2C+b+%5Cin+%5Cmathbf%7BZ%7D%2Cb+%5Cgeq+0+%5Cright%5C%7D+%5Ccup+%5Cleft%5C%7B+%5Cinfty%5Cright%5C%7D&bg=ffffff&fg=000000&s=0&c=20201002) ,
,
![\mathbf{Z^{*}}\left [ i \right ]= \left \{ a+bi : a,b \in \mathbf{Z}, 0\leq a\leq 1, b\geq \left ( a-a^{2} \right )^{1/2} \right \}\cup \left \{ \infty \right \}](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BZ%5E%7B%2A%7D%7D%5Cleft+%5B+i+%5Cright+%5D%3D+%5Cleft+%5C%7B+a%2Bbi+%3A+a%2Cb+%5Cin+%5Cmathbf%7BZ%7D%2C+0%5Cleq+a%5Cleq+1%2C+b%5Cgeq+%5Cleft+%28+a-a%5E%7B2%7D+%5Cright+%29%5E%7B1%2F2%7D+%5Cright+%5C%7D%5Ccup+%5Cleft+%5C%7B+%5Cinfty+%5Cright+%5C%7D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
The set ![\mathbf{Z}[i] , \mathbf{Z}^{*}[i]](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BZ%7D%5Bi%5D+%2C+%5Cmathbf%7BZ%7D%5E%7B%2A%7D%5Bi%5D&bg=ffffff&fg=000000&s=0&c=20201002) and their subdivisions into
and their subdivisions into
![\mathbf{Z}[i] = \mathbf{V_1}\cup \mathbf{V_2}\cup \mathbf{V_3}\cup \mathbf{E_1}\cup \mathbf{E_2}\cup \mathbf{E_3}\cup \mathbf{C},](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BZ%7D%5Bi%5D+%3D+%5Cmathbf%7BV_1%7D%5Ccup+%5Cmathbf%7BV_2%7D%5Ccup+%5Cmathbf%7BV_3%7D%5Ccup+%5Cmathbf%7BE_1%7D%5Ccup+%5Cmathbf%7BE_2%7D%5Ccup+%5Cmathbf%7BE_3%7D%5Ccup+%5Cmathbf%7BC%7D%2C&bg=ffffff&fg=000000&s=0&c=20201002) and
and ![\mathbf{Z}^{*}[i] = \mathbf{V^{*}_1}\cup \mathbf{V^{*}_2}\cup \mathbf{V^{*}_3}\cup\mathbf{C^{*}}.](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BZ%7D%5E%7B%2A%7D%5Bi%5D+%3D+%5Cmathbf%7BV%5E%7B%2A%7D_1%7D%5Ccup+%5Cmathbf%7BV%5E%7B%2A%7D_2%7D%5Ccup+%5Cmathbf%7BV%5E%7B%2A%7D_3%7D%5Ccup%5Cmathbf%7BC%5E%7B%2A%7D%7D.&bg=ffffff&fg=000000&s=0&c=20201002)
are shown in Fig. 1, Fig. 1*, respectively.
 Figure 1, Figure 1*. Every boundary point occurring in Fig. 1 is properly equivalent to a real number, and that every boundary point occurring in Fig. 1* is improperly equivalent to a real number. [1]
Figure 1, Figure 1*. Every boundary point occurring in Fig. 1 is properly equivalent to a real number, and that every boundary point occurring in Fig. 1* is improperly equivalent to a real number. [1]
(Note : all regions are bounded by straight lines or circles with radii  (or part thereof), and are supposed to be closed;
(or part thereof), and are supposed to be closed; 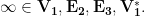 )
)
The 8 matrices  are defined as follows :
are defined as follows :

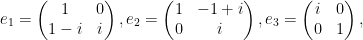
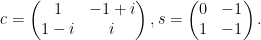
For any invertible matrix M,

with elements in 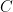 , let
, let  denote the corresponding homographic map :
denote the corresponding homographic map :

And  denotes complex conjugation of
denotes complex conjugation of 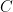 .
.
A homographic map  is called unimodular if
is called unimodular if ![p,q,r,s\in \mathbf{Z}\left [ i \right ]](https://s0.wp.com/latex.php?latex=p%2Cq%2Cr%2Cs%5Cin+%5Cmathbf%7BZ%7D%5Cleft+%5B+i+%5Cright+%5D&bg=ffffff&fg=000000&s=0&c=20201002) (the ring of Gaussian integers) and
(the ring of Gaussian integers) and  . Notice that the determinant of a unimodular map is defined only as an element in the quotient group
. Notice that the determinant of a unimodular map is defined only as an element in the quotient group  consisting of the two elements
consisting of the two elements  . A unimodular map
. A unimodular map  is called properly unimoduIar if
is called properly unimoduIar if 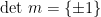 and improperly unimodular if
and improperly unimodular if  .
.
An immediate consequence of these definitions is that every boundary point occurring in Fig. 1 is properly equivalent to a real number, and that every boundary point occurring in Fig. 1* is improperly equivalent to a real number.
A complex number, for example 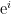 can be represented as a series of these matrices:
can be represented as a series of these matrices:  and so on. Multiplying them together would yield :
and so on. Multiplying them together would yield :

If the top and bottom are added up, the fraction  can be made, which approximately equals
can be made, which approximately equals 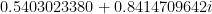 .
.  starts off
starts off  .
.
The Asmus Schmidt method uses partitions to divide the complex plane into regions, then subregions, and so on, and in this way, each point is encoded by the sequence of regions to which it belongs. In the first generation :
 Figure 2. The first generation of Asmus Schmidt’s complex continued fraction method. (picture credite to Ed Pegg Jr., courtesy of MAA)
Figure 2. The first generation of Asmus Schmidt’s complex continued fraction method. (picture credite to Ed Pegg Jr., courtesy of MAA)
After that, each triangular region is divided into 4 parts, by adding a circle. In addition, each circle is divided into 8 regions, by adding 3 tangent circles.
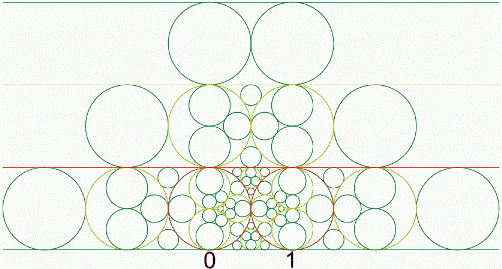
Figure 3. The third generation of Asmus Schmidt’s complex continued fraction method. (picture credite to Ed Pegg Jr., courtesy of MAA)
Here is a portion of fourth generation :

Figure 4. The fourth generation of Asmus Schmidt’s complex continued fraction method. (picture credite to Ed Pegg Jr., courtesy of MAA)
Another interesting visualization on further successive generation was done by Mathematica software[7] in which seven matrices are used. Each use of these matrices divides the plane into seven parts as shown in the Figure 5.

Figure 5. Sucessive generations of Asmus Schmidt’s complex continued fraction method (picture credite to Doug Hensley, at Wolfram Library Archive).
References :
[1] Asmus L. Schmidt, Diophantine Approximation of Complex Numbers, University of Copenhagen, Denmark.
[2] Robert M. Corless, Continued Fractions and Chaos, Dept. Applied Math, University of Western Ontario, Canada.
[3] Ed Pegg Jr., Gaussian Numbers, editorial Math Games, March 15, 2004, MAA.
[4] MathWorld, Continued Fractions, Pi Continued Fraction.
[5] W. F. Hammond, Continued Fractions and the Euclidean Algorithm, Department of Mathematics and Statistics, University at Albany.
[6] Wikipedia, Continued Fraction, Generalized continued fraction, Gaussian integer.
[7] Wolfram Library Archive, Complex Continued Fractions, picture download : PDF document.




 Vesica Piscis, which literally means “the bladder of a fish” in Latin, becames the core of all solids. Image from
Vesica Piscis, which literally means “the bladder of a fish” in Latin, becames the core of all solids. Image from  Vesica Piscis with figures within. Image from
Vesica Piscis with figures within. Image from  Comic : Number line by
Comic : Number line by 







